In this post we will discuss the implementation of GJK (Gilbert-Johnson-Keerthi) and EPA(Expanding Polytope Algorithm) in C++. The projects were created by a team of 3 as part of a class project for Introduction to Computer Graphics at Rutgers University.
Demonstration
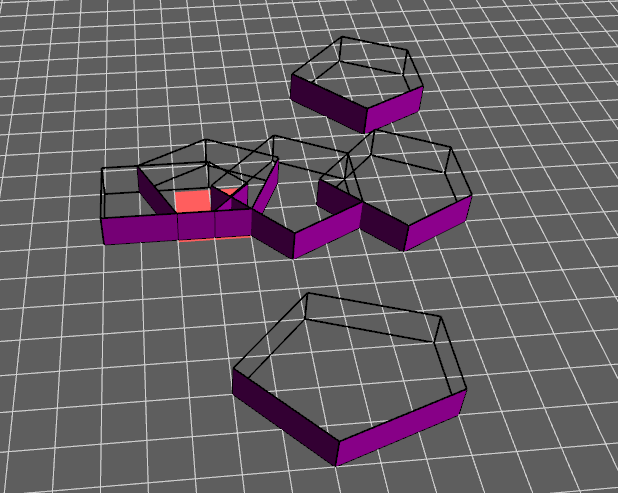
Example 1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
$ ./steersim -testcase polygons1 -ai collisionAI
loaded module collisionAI
loaded module testCasePlayer
Initializing...
Preprocessing...
NO collision detected between polygon No.0 and No.1
NO collision detected between polygon No.0 and No.2
NO collision detected between polygon No.0 and No.3
Collision detected between polygon No.0 and No.4 with a penetration depth of 0.707107 and penetration vector of (0.707107,0,0.707107)
Collision detected between polygon No.0 and No.5 with a penetration depth of 2 and penetration vector of (0,0,-1)
NO collision detected between polygon No.1 and No.2
NO collision detected between polygon No.1 and No.3
NO collision detected between polygon No.1 and No.4
NO collision detected between polygon No.1 and No.5
NO collision detected between polygon No.2 and No.3
NO collision detected between polygon No.2 and No.4
NO collision detected between polygon No.2 and No.5
Collision detected between polygon No.3 and No.4 with a penetration depth of 1 and penetration vector of (-1,0,0)
NO collision detected between polygon No.3 and No.5
Collision detected between polygon No.4 and No.5 with a penetration depth of 1.34164 and penetration vector of (-0.894427,0,-0.447214)
Simulation is running..
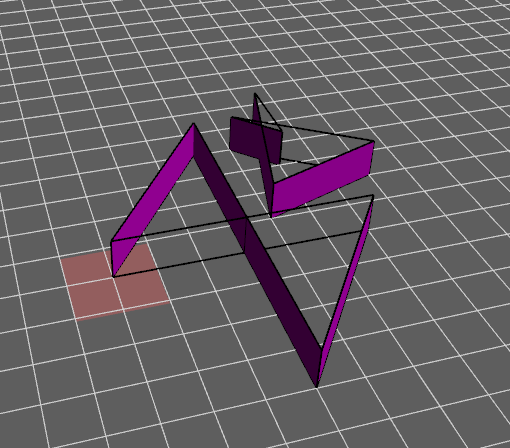
Example 2
1
2
3
4
5
6
7
8
$ ./steersim -testcase polygons2 -ai collisionAI
loaded module collisionAI
loaded module testCasePlayer
Initializing...
Preprocessing...
Collision detected between polygon No.0 and No.1 with a penetration depth of 1 and penetration vector of (-0.8,0,0.6)
Simulation is running...
Fixed test case of Example 2

1
2
3
4
5
6
7
8
9
10
$ ./steersim -testcase polygons2-fixed -ai collisionAI
loaded module collisionAI
loaded module testCasePlayer
Initializing...
Preprocessing...
NO collision detected between polygon No.0 and No.1
NO collision detected between polygon No.0 and No.2
NO collision detected between polygon No.1 and No.2
Simulation is running...
The output for polygons2.xml shows a collision detected, while observing the polygons there is clearly no collision between the two shapes. This is because the shapes are concave, and our implementation is not able to handle this case. Since the usual solution is to have the engine represent concave shapes as multiple convex shapes for the purposes of collision detection, we can manually modify the testcase to represent the same shapes with more polygons.
The fixed version of polygons2 represents the larger “bow tie” shape as two triangles. The smaller shape is unmodified as the first change was sufficient: the output of this fixed case properly shows that there are no collisions between the two (now three) shapes.
Gilbert-Johnson-Keerthi Algorithm
GJK is an algorithm which helps us decide if two shapes are colliding. You need to first create a helper method which will calculate the point that will give the maximum dot product in a particular direction.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int GetFarthestIndexInDirection(Util::Vector direction,const std::vector<Util::Vector>& ShapeA)
{
double MaxDot = direction*ShapeA[0];
int FarthestIndex = 0;
for(unsigned int i = 1; i < ShapeA.size(); i++)
{
double CurrentDot = direction*ShapeA[i];
if(CurrentDot>MaxDot)
{
MaxDot = CurrentDot;
FarthestIndex = i;
}
}
return FarthestIndex;
}
Next we need a support function which will get us our Minkowski Difference. The Minkowski Difference is the subtraction of every point on the boundary of one shape with every point on the boundary of another shape.
1
2
3
4
5
6
7
8
9
10
Util::Vector Support(const std::vector<Util::Vector>& ShapeA,const std::vector<Util::Vector>& ShapeB,Util::Vector direction)
{
Util::Vector FirstPoint = ShapeA[GetFarthestIndexInDirection(direction,ShapeA)];
Util::Vector newDirection = -1 * direction;
Util::Vector SecondPoint = ShapeB[GetFarthestIndexInDirection(newDirection,ShapeB)];
Util::Vector MinkowskiDifference = FirstPoint - SecondPoint;
return MinkowskiDifference;
}
The GJK algorithm checks the Minkowski Difference. If these is an origin in the simplex (a vector full of points), then there is a collision.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
bool GJK(const std::vector<Util::Vector>& ShapeA,const std::vector<Util::Vector>& ShapeB, std::vector<Util::Vector>& simplex)
{
Util::Vector DirectionVector(1,0,-1);
simplex.push_back(Support(ShapeA, ShapeB, DirectionVector));
Util::Vector newDirection = -1 * DirectionVector;
while(true)
{
simplex.push_back(Support(ShapeA,ShapeB, newDirection));
if(simplex.back() * newDirection <= 0)
{
return false;
}
else
{
if(CheckContainsOrigin(newDirection,simplex))
{
return true;
}
}
}
}
The CheckContainsOrigin method checks if the origin is in a triangle formed by 3 points in the simplex The CheckContainsOrigin method is in our github linked on the bottom of this post.
Here is a nice Youtube visualization I found:
Expanding Polytope Algorithm
The steps to compute EPA are as follows:
- Get the nearest Edge to the origin
1
getNearestEdge(simplex, distance, normal, index);
- Find a support point on that point in the direction of the edge’s normal
1
Util::Vector sup = Support(shapeA, shapeB, normal);
- Get the dot product of the support point and the edge’s normal
1
float d = sup*normal;
- If the difference between the distance to nearest edge and dot product is less than 0 then we have the penetration vector equal to the normal of the edge and the penetration depth equal to the distance.
1
2
3
4
5
6
7
8
if(d - distance <= 0)
{
penetration_vector = normal;
penetration_depth = distance;
return true;
}
Helpful link for EPA: Here
Github Link: Here
